Answer:
(a) B. G(x) is an antiderivative of f(x) because G'(x) = f(x) for all x.
(b) Every function of the form
 is an antiderivative of 8x
is an antiderivative of 8x
Explanation:
A function F is an antiderivative of the function f if
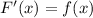
for all x in the domain of f.
(a) If
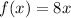 , then
, then
 is an antiderivative of f because
is an antiderivative of f because
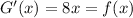
Therefore, G(x) is an antiderivative of f(x) because G'(x) = f(x) for all x.
Let F be an antiderivative of f. Then, for each constant C, the function F(x) + C is also an antiderivative of f.
(b) Because

then
 is an antiderivative of
is an antiderivative of
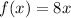 . Therefore, every antiderivative of 8x is of the form
. Therefore, every antiderivative of 8x is of the form
 for some constant C, and every function of the form
for some constant C, and every function of the form
 is an antiderivative of 8x.
is an antiderivative of 8x.