Answer:
the person will be in the shore at 10.73 minutes after launch the shoe.
Step-by-step explanation:
For this we will use the law of the lineal momentum.
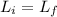
Also,
L = MV
where M is de mass and V the velocity.
replacing,
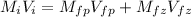
wher Mi y Vi are the initial mass and velocity, Mfp y Vfp are the final mass and velocity of the person and Mfz y Vfz are the final mass and velocity of the shoe.
so, we will take the direction where be launched the shoe as negative. then:
(70)(0) = (70-0.175)(
 ) + (0.175)(-3.2m/s)
) + (0.175)(-3.2m/s)
solving for
 ,
,
 =
=
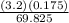
 = 0.008m/s
= 0.008m/s
for know when the person will be in the shore we will use the rule of three as:
1 second -------------- 0.008m
t seconds-------------- 5.15m
solving for t,
t = 5.15m/0.008m
t = 643.75 seconds = 10.73 minutes