Question

Are triangles △ABCtriangle, A, B, C and △DEFtriangle, D, E, F similar? To answer, try to map △ABCtriangle, A, B, C onto △DEFtriangle, D, E, F using the interactive widget.

Answer 1

Answer: Neither

Explanation:

Got it wrong bc of the person it top of me but yea

Answer 2

From three condition the it is proved that Δ ABC and Δ DEF are similar Triangles .

Explanation:

Given as :

To Proof : Triangle Δ ABC and Triangle Δ DEF are similar

There are three methods for two Triangles to be similar

A ) SAS i.e side angle side

B ) AA i.e angle angle

C ) SSS i.e side side side

Now,

A) If two triangle have a pair of equal corresponding angles and sides are proportional then triangle are similar

So, If in Δ ABC and Δ DEF

∠ B = ∠ E

and ,
`(AB)/(DE)` =
`(BC)/(EF)`

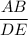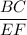
Then Δ ABC
`\sim` Δ DEF

I.e SAS similarity

B ) If two triangles have equal corresponding angles , then triangles are similar .

So, If in Δ ABC and Δ DEF

∠ B = ∠ E and ∠ A = ∠ D

Then Δ ABC
`\sim` Δ DEF

I.e AA similarity

C ) If two triangles have three pairs of corresponding sides proportional then triangles are similar .

So, If in Δ ABC and Δ DEF

`(AB)/(DE)` =
`(BC)/(EF)` =
`(AC)/(DF)`

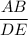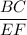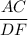
Then Δ ABC
`\sim` Δ DEF

I.e SSS similarity

Hence From three condition the it is proved that Δ ABC and Δ DEF are similar Triangles . answer