Answer:
The length of the altitude is 9.3 yards and
The area of the triangle Δ UVW is 139.3 yd².
Explanation:
Given
WU = 22 yd
WV = 30 yd
∠ UWV = 25°
To Find:
Altitude, UM = ?
area of the Δ UVW = ?
Construction:
Draw UM perpendicular to WV, that is altitude UM to WV.
Solution:
In right triangle Δ UWM if we apply Sine to angle W we get
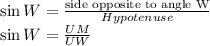
substituting the values we get
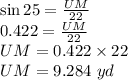
Therefore, the altitude from U to WV is UM = 9.3 yd.(rounded to nearest tenth)
Now for area we have formula

The area of the triangle Δ UVW is 139.3 yd². (rounded to nearest tenth)