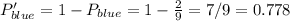Answer:
P(No blue)=7/9=0.778
Explanation:
The sample space of an experiment is "the set of all possible outcomes of that experiment".
The Complement Rule states "that the sum of the probabilities of an event and its complement must equal 1". So for example if A is an event and A' their complement we have this:
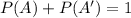
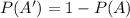
The probability of an event is "a number describing the chance that the event will happen".
For this problem we need to find first the sample space and is given by:
![\Omega = [6white,8Black,4Blue]](https://img.qammunity.org/2020/formulas/mathematics/high-school/wd2ztq59u1etea80tiwdcatdk7t0erk5u2.png) for a total of 18 socks.
for a total of 18 socks.
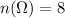
We can use the definition of probability of an event, and we find the probability that the randomly select sock would be blue we have:
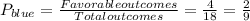
And then using the complement rule if we want the probability that the randomly selected sock would be NOT blue we have: