Question

A food safety guideline is that the mercury in fish should be below 1 part per million​ (ppm). Listed below are the amounts of mercury​ (ppm) found in tuna sushi sampled at different stores in a major city. Construct a 90​% confidence interval estimate of the mean amount of mercury in the population.

0.60 0.74 0.09 0.89 1.31 0.51 0.94


What is the confidence interval estimate of the population mean?


______ppm < u < ______ppm

(Round to three decimal places as needed)


Does it appear that there is too much mercury in tuna​ sushi?

Answer 1

Confidence Interval: (0.44,1.00)

Explanation:

We are given the following data set:

0.60, 0.74, 0.09, 0.89, 1.31, 0.51, 0.94

Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

where
`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(:5.08)/(7) = 0.725`

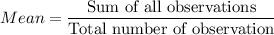
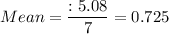
Sum of squares of differences = 0.8809

`S.D = \sqrt{(0.8809)/(6)} = 0.383`

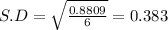
90% Confidence interval:

`\bar{x} \pm t_(critical)\displaystyle(s)/(√(n))`

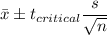
Putting the values, we get,

`t_(critical)\text{ at degree of freedom 6 and}~\alpha_(0.10) = \pm 1.943`

`0.725 \pm 1.943((0.383)/(√(7)) ) =0.725 \pm 0.2812 = (0.44,1.00)`

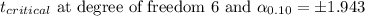
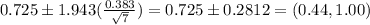
No, it does not appear that there is too much mercury in tuna​ sushi.