Answer:
rate of return is 7.56 %
Step-by-step explanation:
given data
annual cash flows C1 = $36,800
annual cash flows C2 = $45,500
annual cash flows C3 = $56,200
annual cash flows C4 = $21,800
initial cost = $135,000
to find out
internal rate of return
solution
we will apply here initial cost formula for all annual cash flow that is express as
initial cost =
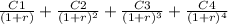 .......................1
.......................1
here C is annual cash flow and r is rate of return
put here value and we get r
initial cost =
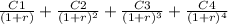
135000 =
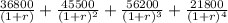
solve it and we get
r = 0.0756
so rate of return is 7.56 %