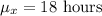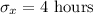Question

A group of friends has gotten very competitive with their board game nights. They have found that overall, they each have won an average of 18 games, with a population standard deviation of 6 games. If a sample of only 2 friends is selected at random from the group, select the expected mean and the standard deviation of the sampling distribution from the options below. Remember to round to the nearest whole number.

Answer 1

Answer:
`\mu_x=18\text{ hours}`

`\sigma_x=4\text{ hours}`

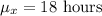
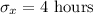
Explanation:

We know that mean and standard deviation of sampling distribution is given by :-

`\mu_x=\mu`

`\sigma_x=(\sigma)/(√(n))`

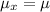
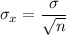
, where
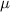`\mu` = population mean

`\sigma` =Population standard deviation.

n= sample size .

In the given situation, we have

`\mu=18\text{ hours}`

`\sigma=6\text{ hours}`

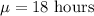
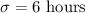
n= 2

Then, the expected mean and the standard deviation of the sampling distribution will be :_

`\mu_x=\mu=18\text{ hours}`

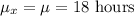
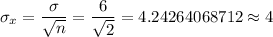`\sigma_x=(\sigma)/(√(n))=(6)/(√(2))=4.24264068712\approx4` [Rounded to the nearest whole number]

Hence, the the expected mean and the standard deviation of the sampling distribution :

`\mu_x=18\text{ hours}`

`\sigma_x=4\text{ hours}`