Question

A vehicle moves with a velocity, v(t) = exp(0.2t) - 1, 0 ≤ t ≤ 5 s. Peter would like to calculate the displacement of the vehicle as a function of time, x(t), by integrating given velocity over the time from t = 0. Use t = 0.2 s for trapezoidal rule.

Answer 1

`x|_0^(0.2)=1.59535`

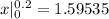
Step-by-step explanation:

Given expression of velocity:

`v(t)=10^(0.2t)-1 ;\ \ 0\leq t\leq 5\ s`

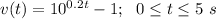
For getting displacement we need to integrate the above function with respect to t.

Given period of integration:

`t_0=0\ s \to t_f=0.2\ s`

For trapezoidal rule we break the given interval into two parts of 0.1 s each.

∴take n=2

hence,
`\Delta t= 0.1`

`v(0)=0`

`v(0.1)=1.0471`

`v(0.2)=1.0965`

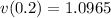
Now, using trapezoidal rule:

`\int_(0)^(0.2)v(t)\ dt=\Delta x[(1)/(2)* v(0)+v(0.1)+(1)/(2)* v(0.2)]`

`\int_(0)^(0.2)v(t)\ dt=0.1 [(1)/(2)* 0+1.0471+(1)/(2)* 1.0965]`

`x|_0^(0.2)=1.59535`

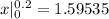
Note:Smaller the value of sub-interval better is the accuracy.