Number of subscriber the magazine will have after 3 years from now approximately be 8767
Solution:
Given that magazine currently has 8700 subscribers for its online web version
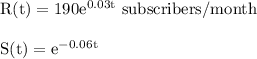
After 3 years, time(t) = 36 month
Total number of subscribers after 3 years from now :
Substitute "t" = 36
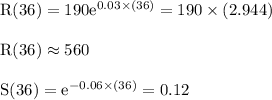
Subscribers remaining = 0.12 x 560 = 67.2
The magazine currently has 8700 subscribers
Added Subscriber = 8700 + 560 = 9260
Remaining Subscriber = 8700 + 67.2 = 8767.2
Therefore number of subscriber the magazine will have after 3 years from now approximately be 8767