Question

Tain has a great literary tradition that spans centuries. One might assume, then, that Britons read more than citizens of other countries. Some Canadians, however, feel that a higher percentage of Canadians than Britons read. A recent Gallup Poll reported that 86% of 1004 randomly sampled Canadians read at least one book in the past year, compared to 81% of 1009 randomly sampled Britons. Do these results confirm a higher reading rate in Canada?

1) Test an appropriate hypothesis and state your conclusions

Answer 1

Null hypothesis:
`p_(1) \leq p_(2)`

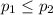
Alternative hypothesis:
`p_(1) > p_(2)`

`z=3.02`

`p_v =P(Z>3.02)=0.00127`

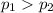
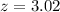
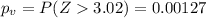
The p value is a very low value and using any significance level for example
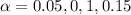`\alpha=0.05, 0,1,0.15` always
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, and we can say the the proportion of Canadians is not significantly higher than the porportions of readers at Britons.

Explanation:

1) Data given and notation

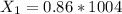`X_(1)=0.86*1004` represent the number of Canadians randomly sampled by Gallup that read at least one book in the past year

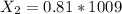`X_(2)=0.81*1009` represent the number of Britons randomly sampled that read at least one book in the past year

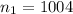`n_(1)=1004` sample of Gallup selected

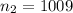`n_(2)=1009` sample of Britons selected

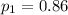`p_(1)=0.86` represent the proportion of Canadians randomly sampled by Gallup that read at least one book in the past year

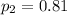`p_(2)=0.81` represent the proportion of Britons randomly sampled that read at least one book in the past year

z would represent the statistic (variable of interest)

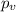`p_v` represent the value for the test (variable of interest)

2) Concepts and formulas to use

We need to conduct a hypothesis in order to check if the proportion for men with red/green color blindness is a higher than the rate for women , the system of hypothesis would be:

Null hypothesis:
`p_(1) \leq p_(2)`

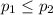
Alternative hypothesis:
`p_(1) > p_(2)`

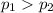
We need to apply a z test to compare proportions, and the statistic is given by:

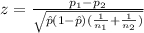`z=\frac{p_(1)-p_(2)}{\sqrt{\hat p (1-\hat p)((1)/(n_(1))+(1)/(n_(2)))}}` (1)

Where
`\hat p=(X_(1)+X_(2))/(n_(1)+n_(2))=(0.81+0.86)/(2)=0.835`

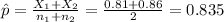
3) Calculate the statistic

Replacing in formula (1) the values obtained we got this:

`z=\frac{0.86-0.81}{\sqrt{0.835(1-0.835)((1)/(1004)+(1)/(1009))}}=3.02`

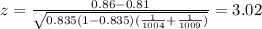
4) Statistical decision

For this case we don't have a significance level provided
`\alpha`, but we can calculate the p value for this test.

Since is a one side test the p value would be:

`p_v =P(Z>3.02)=0.00127`

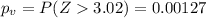
So the p value is a very low value and using any significance level for example
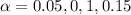`\alpha=0.05, 0,1,0.15` always
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, and we can say the the proportion of Canadians is not significantly higher than the porportions of readers at Britons.