Question

A man starts walking from home and walks 2 miles at 20° north of west, then 4 miles at 10° west of south, then 3 miles at 15° north of east. If he walked straight home,

(a)-how far would he have to walk?

(b)-In what direction would he have to walk?

Answer 1

a) R = 2.5 mi b) To return to your case you must walk in the opposite direction or θ = 98º

This is 8º north west

Step-by-step explanation:

This is a distance exercise with vectors the best way to work these is to decompose the vectors and perform the sum on each axis separately

To use the Cartesian system all angles must be measured from the positive side of the x-axis or the signs of the components must be assigned manually depending on the quadrant where they are.

First vector A = 2 to 20º north west

Measured from the positive x axis is θ = 180 -20 = 160º

We use trigonometry to find the components

Cos 20 = Aₓ / A

sin 20 =
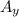`A_(y)` / A

Aₓ = A cos 160 = 2 cos 160

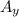`A_(y)` = A sin160 = 2 sin160

Aₓ = -1,879 mi

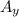`A_(y)` = 0.684 mi

Second vector B = 4 mi 10º west of the south

Angle θ = 270 - 10 = 260º

cos 2600 = Bₓ / B

sin 260 =
`B_(y)` / B

Bₓ = B cos 260

`B_(y)` = B sin 260

Bₓ = 4 cos 260

`B_(y)` = 4 sin 260

Bₓ = -0.6946mi

`B_(y)` = - 3,939 mi

Third vector C = 3 mi to 15 north east

cos 15 = Cₓ / C

sin15 =
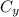`C_(y)` / C

Cₓ = C cos 15

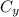`C_(y)` = C sin15

Cₓ = 3 cos 15

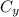`C_(y)` = 3 sin 15

Cₓ = 2,898 mi

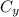`C_(y)` = 0.7765 mi

Now we can find the final position of the person

X = Aₓ + Bₓ + Cₓ

X = -1.879 -0.6949 + 2.898

X = 0.3241 mi

Y =
`A_(y)` +
`B_(y)` +
`C_(y)`

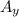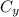
Y = 0.684 - 3.939 +0.7765

Y = -2.4785 mi

a) We use Pythagoras' theorem

R = √ (x2 + y2)

R = √ (0.3241 2 + (-2.4785) 2)

R = 2.4996 mi

R = 2.5 mi

b) let's use trigonometry

Tan θ = y / x

Tanθ = -2.4785 / 0.3241

θ = tan⁻¹ (-7,647)

θ = -82

Measured from the positive side of the x axis is Te = 360 - 82 = 278º

(90-82) south east

To return to your case you must walk in the opposite direction or Te = 98º

This is 8º north west