Question

Calculate the work required to move a planet’s satellite of mass 1820 kg from a circular orbit of radius 2R to one of radius 3R, where 7.37×106 m is the radius of the planet. The mass of the planet is 7.51 × 1024 kg. Answer in units of J.

Answer 1

The work required to move a planet's satellite is W = 2854.61 J

Step-by-step explanation:

Given data,

The mass of the satellite, m = 1820 kg

The radius of the circular orbit, r = 2R

The radius of the planet, r = 5.37 x 10⁶ m

The mass of the planet, M = 7.5 x 10²⁴ kg

The formula for work done from the 2R to 3R is,

W =
`\int_(2R)^(3R)(GMm)/(r^(2))dr`

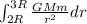
W = GMm/3R - GMm/2R

W = (-0.17)GMm/R J

The negative sign indicates that the energy stored in the satellite as the potential energy.

Substituting the values

W = (-0.17) 6.673 x 10⁻¹¹ X 7.51 x 10²⁴ X 1820 / (7.37 x 10⁶)²

= -2854.61 J

Hence, the work required to move a planet's satellite is W = 2854.61 J