Question

A solid sphere is released from the top of a ramp that is at a height h1 = 2.30 m. It rolls down the ramp without slipping. The bottom of the ramp is at a height of h2 = 1.69 m above the floor. The edge of the ramp is a short horizontal section from which the ball leaves to land on the floor. The diameter of the ball is 0.17 m.

Answer 1

The horizontal distance d does the ball travel before landing is 1.72 m.

Step-by-step explanation:

Given that,

Height of ramp
`h_(1)=2.30\ m`

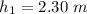
Height of bottom of ramp
`h_(2)=1.69\ m`

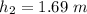
Diameter = 0.17 m

Suppose we need to calculate the horizontal distance d does the ball travel before landing?

We need to calculate the time

Using equation of motion

`h_(2)=ut+(1)/(2)gt^2`

`t=\sqrt{(2h_(2))/(g)}`

`t=\sqrt{(2*1.69)/(9.8)}`

`t=0.587\ sec`

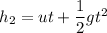
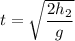
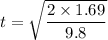
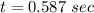
We need to calculate the velocity of the ball

Using formula of kinetic energy

`K.E=(1)/(2)mv^2+(1)/(2)I\omega^2`

`K.E=(1)/(2)mv^2+(1)/(2)*((2)/(5)mr^2)*((v)/(r))^2`

`K.E=(7)/(10)mv^2`

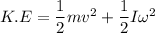
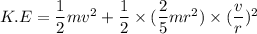
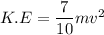
Using conservation of energy

`K.E=mg(h_(1)-h_(2))`

`(7)/(10)mv^2=mg(h_(1)-h_(2))`

`v^2=(10)/(7)* g(h_(1)-h_(2))`

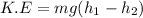
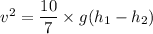
Put the value into the formula

`v=\sqrt{(10*9.8*(2.30-1.69))/(7)}`

`v=2.922\ m/s`

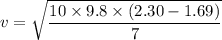
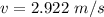
We need to calculate the horizontal distance d does the ball travel before landing

Using formula of distance

`d =vt`

Where. d = distance

t = time

v = velocity

Put the value into the formula

`d=2.922* 0.587`

`d=1.72\ m`

Hence, The horizontal distance d does the ball travel before landing is 1.72 m.