Question

A polymer is manufactured in a batch chemical process. Viscosity measurements show that it is approximately normally distributed with a standard deviation of 20. A random sample of 42 batches has a mean viscosity of 759. Construct a 99% confidence interval around the true population mean viscosity.

Answer 1

Answer: (751.05, 766.95)

Explanation:

We know that the confidence interval for population mean is given by :-

`\overline{x}\pm z*(\sigma)/(√(n))`,

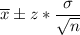where
`\sigma` =population standard deviation.

`\overline{x}`= sample mean

n= sample size

z* = Two-tailed critical z-value.

Given :
`\sigma= 20`

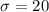
n= 42

`\overline{x}=759`

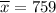
We know that from z-table , the two-tailed critical value for 99% confidence interval : z* =2.576

Now, the 99% confidence interval around the true population mean viscosity :-

`759\pm (2.5760)(20)/(√(42))\\\\=759\pm (2.5760)(3.086067)\\\\=759\pm7.9497=(759-7.9497,\ 759+7.9497)\]\\=(751.0503,\ 766.9497)\approx(751.05,\ 766.95)`

∴ A 99% confidence interval around the true population mean viscosity : (751.05, 766.95)