Question

Standing at a crosswalk, you hear a frequency of 540 Hz from the siren of an approaching ambulance. After the ambulance passes, the observed frequency of the siren is 446 Hz. Determine the ambulance's speed from these observations. (Take the speed of sound to be 343 m/s.)

Answer 1

Speed of the ambulance is 32.7 metres per second.

Step-by-step explanation:

Let the actual frequency of the siren be
`f_(0)`.

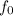Frequency observed by me when ambulance is approaching = 540 Hz

Frequency observed by me when ambulance is moving away = 446 Hz

Let
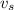`v_(s)` be the speed of sound and
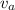`v_(a)` be the speed of ambulance.Then according to Doppler effect:

When source is moving towards observer,frequency observed is given as

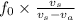`f_(0) * (v_(s) )/(v_(s) - v_(a) )` = 540 Hz

When source is moving away from observer,frequency observed is given as

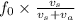`f_(0) * (v_(s) )/(v_(s) + v_(a) )` = 446 Hz

Taking
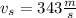`v_(s) = 343 (m)/(s)` and solving the above two equations by eliminating
`f_(0)`,

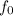we get
`v_(a) = 32.7 (m)/(s)`