(a) 1000
(b) 11100
(c) 11095.
Step-by-step explanation:
(a) If A1 is a subset of A2 and A2 is a subset of A3, then all the elements of A1 are in A2 and all the elements of A2 are in A3.
Then, n(A1 n A2) = 100, n(A2 n A3) = 1000 , n(A1 n A3) = 100 and n(A1 n A2 n A3) = 100.
So, we get
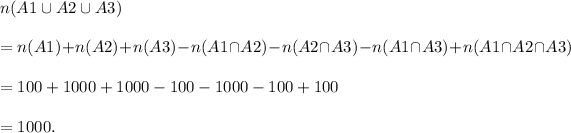
(b) If the sets are pairwise disjoint, then
n(A1 n A2) = n(A2 n A3) = n(A1 n A3) = n(A1 n A2 n A3) = 0.
So, we get

(c) If there are two elements common to each pair of sets and one element in all three sets, then
n(A1 n A2) = 2, n(A2 n A3) = 2, n(A1 n A3) = 2 and n(A1 n A2 n A3) = 1.
So, we get
