To solve this problem it is necessary to apply the concepts related to the acceleration of gravity due to the force exerted by a start and the calculation of angular velocity as a function of acceleration and radius.
By definition we know that the acceleration exerted by the celestial body is given under the equation

Where,
G = Gravitational Universal Constant
M = Mass
R = Radius
The radius of Europa is
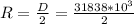

Applying the gravitational equation,


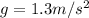
Therefore the angular acceleration can be obtained through the kinematic equation
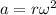
Where,
a = acceleration
r = length of the arm
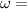 Angular acceleration
Angular acceleration
As a = g then,
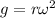
Where,
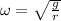
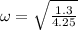
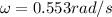
Therefore the angular speed of arm is 0.553rad/s