Question

How many molecules of N2 are in a 400.0 mL container at 780 mm Hg and 135°C? Avogadro’s number = 6.022 x 1023A) 7.01 × 1021 moleculesB) 7.38 × 1021 moleculesC) 2.12 × 1022 moleculesD) 2.23 × 1022 molecules

Answer 1

B

Step-by-step explanation:

Firstly, we will need to calculate the number of moles. To do this, we make use of the ideal gas equation

PV = nRT

n = PV/RT

The parameters have the following values according to the question:

P = 780mmHg, we convert this to pascal.

760mHG = 101325pa

780mmHg = xpa

x = (780 * 101325)/760 = 103,991 Pa

V= 400ml = 0.4L

T = 135C = 135 + 273.15 = 408.15K

n = ?

R = 8314.463LPa/K.mol

Substituting these values into the equation yields the following:

n = (103991 * 0.4)/(8314.463 * 408.15)

= 0.012 moles

Now we know 1 mole contains 6.02 * 10^23 molecules, hence, 0.012moles will contain = 0.012 * 6.02 * 10^23 = 7.38 * 10^21 molecules

Answer 2

Answer: The number of nitrogen molecules in the container are
`7.38* 10^(21)`

Step-by-step explanation:

To calculate the moles of gas, we use the equation given by ideal gas which follows:

`PV=nRT`

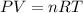
where,

P = pressure of the gas = 780 mmHg

V = Volume of the gas = 400.0 mL = 0.4 L (Conversion factor: 1 L = 1000 mL)

T = Temperature of the gas =
`135^oC=[135+273]K=408K`

R = Gas constant =
`62.364\text{ L.mmHg }mol^(-1)K^(-1)`

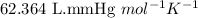
n = number of moles of nitrogen gas = ?

Putting values in above equation, we get:

`780mmHg* 0.4L=n* 62.364\text{ L. mmHg }mol^(-1)K^(-1)* 408K\\\\n=(780* 0.4)/(62.364* 408)=0.01226mol`

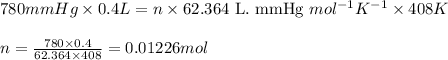
According to mole concept:

1 mole of a compound contains
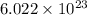`6.022* 10^(23)` number of molecules

So, 0.01226 moles of nitrogen gas will contain =
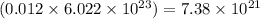`(0.012* 6.022* 10^(23))=7.38* 10^(21)` number of molecules

Hence, the number of nitrogen molecules in the container are
`7.38* 10^(21)`