Question

Listed below are the number of years it took for a random sample of college students to earn bachelor's degrees (based on data from the National Center for Education Statistics). 4, 4, 4, 4, 4, 4, 4.5, 4.5, 4.5, 4.5, 4.5, 4.5, 6, 6, 8, 9, 9, 13, 13, 15

(a) Calculate the sample mean and standard deviation.
(b) Calculate the standard error, SE.
(c) What is the point estimate for the mean time required for all college students to earn bachelor's degrees?
(d) Construct the 90% confidence interval estimate of the mean time required for all college students to earn bachelor's degrees.
(e) Does the confidence interval contain the value of 4 years? Is there anything about the data that would suggest that the confidence interval might not be a good result?

Answer 1

a) Mean = 6.5, sample standard deviation = 3.50

b) Standard error = 0.7826

c) Point estimate = 6.5

d) Confidence interval: (5.1469 ,7.8531)

Explanation:

We are given the following data set for students to earn bachelor's degrees.

4, 4, 4, 4, 4, 4, 4.5, 4.5, 4.5, 4.5, 4.5, 4.5, 6, 6, 8, 9, 9, 13, 13, 15

a) Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

where
`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(130)/(20) = 6.5`

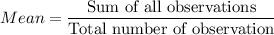
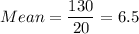
Sum of squares of differences = 6.25 + 6.25 + 6.25 + 6.25 + 6.25 + 6.25 + 4 + 4 + 4 + 4 + 4 + 4 + 0.25 + 0.25 + 2.25 + 6.25 + 6.25 + 42.25 + 42.25 + 72.25 = 233.5

`S.D = \sqrt{(233.5)/(19)} = 3.50`

b) Standard Error

`= \displaystyle(s)/(√(n)) = (3.50)/(√(20)) = 0.7826`

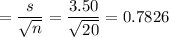
c) Point estimate for the mean time required for all college is given by the sample mean.

`\bar{x} = 6.5`

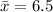
d) 90% Confidence interval:

`\bar{x} \pm t_(critical)\displaystyle(s)/(√(n))`

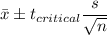
Putting the values, we get,

`t_(critical)\text{ at degree of freedom 19 and}~\alpha_(0.10) = \pm 1.729`

`6.5 \pm 1.729((3.50)/(√(20)) ) = 6.5 \pm 1.3531 = (5.1469 ,7.8531)`

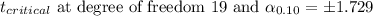
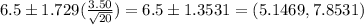
e) No, the confidence interval does not contain the value of 4 years. Thus, confidence interval is not a good estimator as most of the value in the sample is of 4 years. Most of the sample does not lie in the given confidence interval.