Answer:
$10496.77
Explanation:
We have been given that Barbara puts $200 into an account every month that pays 4.5% interest, compounded monthly.
To find the money in the account after 4 years, we will use future value formula.
 , where,
, where,
R = Regular deposits,
r = Interest rate in decimal form
n = Number of times interest in compounded per year,
t = Time in years.
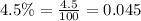
Substitute given values:
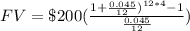
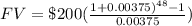
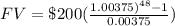
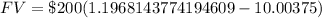
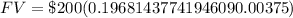
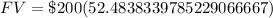
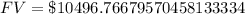
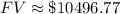
Therefore, there will be an amount of $10496.77 in the account after 4 years.