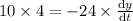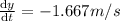Question

A ladder 26 feet long leans against a wall. The foot of the ladder is being drawn away from the wall at a rate of 4 ft/sec. How fast is the top of the ladder sliding down the wall at the instant when the foot of the ladder is 10 ft from the wall?

Answer 1

Answer:1.67 m/s

Step-by-step explanation:

Given

length of ladder L=26 feet

velocity with which bottom is withdrawn is 4 ft/s

when bottom of ladder is at a distance of 10 ft away from wall then top of ladder from bottom is given by

`y^2=26^2-10^2`

`y=24 ft`

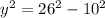
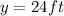
from diagram

`x^2+y^2=L^2`

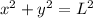
Differentiate w.r.t time we get

`2x\frac{\mathrm{d} x}{\mathrm{d} t}+2y\frac{\mathrm{d} y}{\mathrm{d} t}=0`

`x\frac{\mathrm{d} x}{\mathrm{d} t}=-y\frac{\mathrm{d} y}{\mathrm{d} t}`

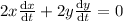
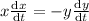
at x=10 ft, y=24 ft

`10* 4=-24* \frac{\mathrm{d} y}{\mathrm{d} t}`

`\frac{\mathrm{d} y}{\mathrm{d} t}=-1.667 m/s`