Question

Translate to a system of equations: Daniela invested a total of $50,000, some in a certificate of deposit (CD) and the remainder in bonds. The amount invested in bonds was $5,000 more than twice the amount she put into the CD. How much did she invest in each account? Call the amount that Daniela invested in the CD d and the amount she invested in bonds b.

Answer 1

Daniela invested $35,000 in bonds and $15,000 in a certificate of deposit (CD)

Explanation:

We call d the amount Daniela invested in the certificate of deposit (CD) and b the amount she invested in bonds.

The first conditions of the problem is the total amount invested is $50,000, so

`d+b=50,000`

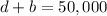
The second demands that the amount invested in bonds was $5,000 more than twice the amount she put into the CD

`b=5,000+2d`

a)

The system of equations is

`\left\{\begin{matrix}d+b=50,000\\ b=5,000+2d\end{matrix}\right.`

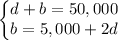
b) To solve the system, we take b from the last equation and replace it in the first equation:

`d+5,000+2d=50,000`

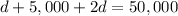
Rearranging

`3d=45,000`

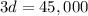
Solving

`d=45,000/3=15,000`

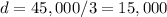
And

`b=5,000+2(15,000)=35,000`

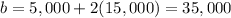
Answer:

Daniela invested $35,000 in bonds and $15,000 in a certificate of deposit (CD)