Question

A coin with a diameter of 2.11 cm is dropped onto a horizontal surface. The coin starts out with an initial angular speed of 19.0 rad/s and rolls in a straight line without slipping. If the rotation slows with an angular deceleration of 1.26 rad/s2 , how far does the coin roll before coming to rest?

Answer 1

9.49596 m

Step-by-step explanation:

`\omega_f` = Final angular velocity = 0

`\omega_i` = Initial angular velocity = 19 rad/s

`\alpha` = Angular acceleration = -1.26 rad/s²

`\theta` = Angle of rotation

Equation of rotational motion

`\omega_f^2-\omega_i^2=2\alpha \theta\\\Rightarrow \theta=(\omega_f^2-\omega_i^2^2)/(2\alpha)\\\Rightarrow \theta=(0^2-19^2)/(2* -1.26)\\\Rightarrow \theta=143.25396\ rad`

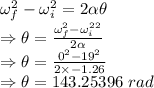
Converting to m

`143.25396* \pi d=143.25396* \pi* 0.0211=9.49596\ m`

The distance the coin rolls before it stops is 9.49596 m