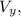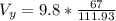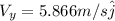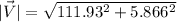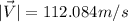Question

You are watching an archery tournament when you start wondering how fast an arrow is shot from the bow. Remembering your physics, you ask one of the archers to shoot an arrow parallel to the ground. Unfortunately the archer stands on an elevated platform of unknown height. However, you find the arrow stuck in the ground 67.0 m away, making a 3.00 ∘ angle with the ground.How fast was the arrow shot?

Answer 1

To develop this problem it is necessary to apply the kinematic equations that describe displacement, velocity and clarification.

By definition we know that velocity is defined as the change of position due to time, therefore

`V = (d)/(t)`

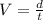
Where,

d = Distance

t = Time

Speed can also be expressed in vector form through its components
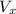`V_x` and
`V_y`

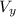
In the case of the horizontal component X, we have to

`V_x = (d)/(t)`

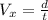
Here d means the horizontal displacement, then

`t = (d)/(V_x)`

`t = (67)/(V_x)`

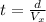
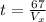
At the same time we have that the vertical component of the velocity is

`V_y = gt`

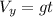
Here,

g = Gravity

Therefore using the relation previously found we have that

`V_y = g (67)/(V_x)`

The relationship between the two velocities and the angle can be expressed through the Tangent, therefore

`tan\theta = (V_y)/(V_x)`

`tan \theta = (g (67)/(V_x) )/(V_x)`

`tan 3 = (9.8(67)/(V_x) )/(V_x)`

`tan 3 = (9.8*67)/(V_x^2)`

`V_x^2 = (9.8*67)/(tan 3)`

`V_x= \sqrt{ (9.8*67)/(tan 3)}`

`V_x = 111.93m/s \hat{i}`

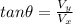
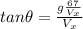
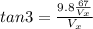
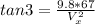
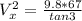
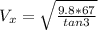
This is the horizontal component, we could also find the vertical speed and the value of the total speed with the information given,

Then
`V_y,`

`V_y = g (67)/(V_x)`

`V_y = 9.8*(67)/(111.93)`

`V_y = 5.866m/s\hat{j}`

`|\vec{V}| = √(111.93^2+5.866^2)`

`|\vec{V}| = 112.084m/s`