Question

A bicycle wheel, of radius 0.300 m and mass 1.23 kg (concentrated on the rim), is rotating at 4.00 rev/s. After 52.2 s the wheel comes to a stop because of friction. What is the magnitude of the average torque due to frictional forces?

Answer 1

T = 0.0266 N*m

Step-by-step explanation:

we know that:

∑T = Iα

Where T is the torque, I is the moment of inertia and α is the angular aceleration.

first, we have to express in radians the angular velocity:

W =
`4*2\pi`

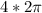
w = 25.132 m/s

with this result, the time t and using the next equation we can find the angular aceleration (α) as;

w = -αt

α =
`(w)/(t)`

α = -
`(25.132)/(52.2)`

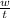
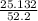
α = -0.481 rad/
`s^2`

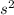
Also, we have to find the moment of inertia following the next equation:

I =
`(1)/(2)MR^2`

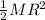
Where M is the mass and R is the radio of the wheel, so replacing the values, we get:

I =
`(1)/(2)(1.23)(0.3)^2`

I = 0.05535

now, we have to go back to the first equation ( ∑T = Iα) and replace the data as:

T = Iα

T = 0.05535(0.481)

T = 0.0266 N*m