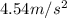Question

A horse of mass 242 kg pulls a cart of mass 224 kg. The acceleration of gravity is 9.8 m/s 2 . What is the largest acceleration the horse can give if the coefficient of static friction between the horse’s hooves and the road is 0.894? Answer in units of m/s 2 .

Answer 1

To solve this problem it is necessary to apply the concepts related to Newton's second Law and the force of friction. According to Newton, the Force is defined as

F = ma

Where,

m= Mass

a = Acceleration

At the same time the frictional force can be defined as,

`F_f = \mu N`

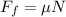
Where,

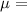`\mu =` Frictional coefficient

N = Normal force (mass*gravity)

Our values are given as,

`m_h = 242 kg\\m_c = 224 kg\\\mu = 0.894\\`

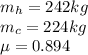
By condition of Balance the friction force must be equal to the total net force, that is to say

`F_(net) = F_f`

`m_(total)a = \mu m_hg`

`(m_h+m_c)a = \mu*m_h*g`

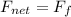
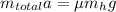
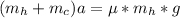
Re-arrange to find acceleration,

`a= (\mu*m_h*g)/((m_h+m_c))`

`a = (0.894*242*9.8)/((242+224))`

`a = 4.54 m/s^2`

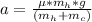
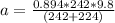
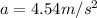
Therefore the acceleration the horse can give is
`4.54m/s^2`