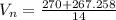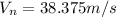Answer:
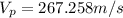
Step-by-step explanation:
using the law of the conservation of the linear momentum:
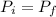
where
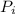 is the inicial momemtum and
is the inicial momemtum and
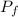 is the final momentum
is the final momentum
the linear momentum is calculated by the next equation
P = MV
where M is the mass and V is the velocity.
so:
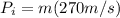
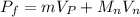
where m is the mass of the proton and
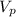 is the velocity of the proton after the collision,
is the velocity of the proton after the collision,
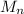 is the mass of the nucleus and
is the mass of the nucleus and
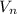 is the velocity of the nucleus after the collision.
is the velocity of the nucleus after the collision.
therefore, we can formulate the following equation:
m(270 m/s) = m
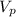 + 14m
+ 14m
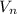
then, m is cancelated and we have:
270 =
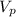 +
+
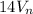
This is a elastic collision, so the kinetic energy K is conservated. Then:
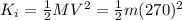
and
Kf =
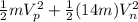
then,
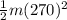 =
=
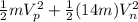
here we can cancel the m and get:
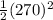 =
=
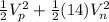
now, we have two equations and two incognites:
270 =
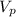 +
+
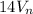 (eq. 1)
(eq. 1)
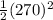 =
=
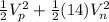
in the second equation, we have:
36450 =
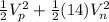 (eq. 2)
(eq. 2)
from this last equation we solve for
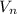 as:
as:
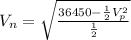
and replace in the other equation as:
270 =
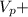 14
14
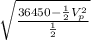
so,
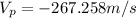
Vp is negative because the proton go in the -i hat direction.
Finally, replacing this value on eq. 1 we get: