Question

Y = x —6x+8 The equation above represents a parabola in the xy-plane. Which of the following equivalent forms of the equation displays the x-intercepts of the parabola as constants or coefficients?

Answer 1

`y=(x-4)(x-2)`

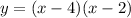
Explanation:

Consider the given equation

`y=x^2-6x+8`

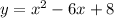
Factor form of a parabola: It displays the x-intercepts.

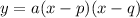`y=a(x-p)(x-q)` .... (1)

where, a is a constant and, p and q are x-intercepts.

So, we need to find the factored form of the given equation.

Splinting the middle term we get

`y=x^2-4x-2x+8`

`y=x(x-4)-2(x-4)`

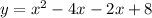
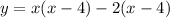
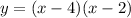`y=(x-4)(x-2)` .... (2)

On comparing (1) and (2) we get

`p=4,q=2`

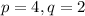
It means x-intercepts of the given parabola are 4 and 2.

Therefore, equivalent forms of the equation is y=(x-4)(x-2).