Question

Three printing presses, R, S, and T, working together at their respective constant rates, can do a certain printing job in 4 hours. S and T, working together at their respective constant rates, can do the same job in 5 hours. How many hours would it take R, working alone at its constant rate, to do the same job?

Answer 1

Press R will take 20 hours.

Explanation:

Given,

The time taken by R, S and T when they work together = 4 hours,

So, the one hour work of R, S and T =
`(1)/(4)`,

Time taken by S and T when they work together = 5 hours,

So, the one hour work of S and T =
`(1)/(5)`

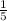
∵ One hour work of R= One hour work of R, S and T - one hour work of S and T

`=(1)/(4)-(1)/(5)`

`=(5-4)/(20)`

`=(1)/(20)`

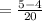
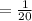
Hence, the time taken ( in hours ) by R when it works alone

`=\frac{1}{\text{One hour work}}`

`=(1)/(1/20)`

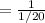
= 20 hours