Question

Suppose you did a hypothesis test using a one-factor ANOVA that produces an F-ratio of F = 3.51. If you tested at alpha, α = 0.05 and the degrees of freedom for the study are df = 2, 18, what is the best decision regarding the null hypothesis?

Answer 1

`p_v=P(F|2,18 >3.51)= 0.0516`

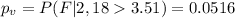
If we analyze the p value and the significance level given we see that
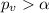`p_v>\alpha` so we have enough evidence to FAIL to reject the null hypothesis. So there is no evidence to conclude that at least one mean of the groups differs significantly from the others.

Explanation:

Analysis of variance (ANOVA) is "a statistical technique that is used to check if the means of two or more groups are significantly different from each other. ANOVA checks the impact of one or more factors by comparing the means of different samples".

The null hypothesis on this case would be:

Null hypothesis:
`\mu_0 =\mu_1 =\mu_2`

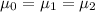
Alternative hypothesis: At least one mean is different from the other's.

We know that we have 3 groups based on the degrees of freedom for the statistic F. Since we know that F=3.51, df=2,18.

The degrees of freedom for the numerator are given by k-1=2, if we solve for k=2+1=3. And k represent the number of groups analyzed.

The degrees of freedom for the denominator are given by N-k=18, since k=3 then N=18+3=21. And that represent the number of total people analyzed.

In order to take a decision respect the null hypothesis we can calculate the p value or the critical value.

If we find the p value we got:

`p_v=P(F|2,18 >3.51)= 0.0516`

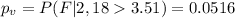
And if we analyze the p value and the significance level given we see that
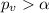`p_v>\alpha` so we have enough evidence to FAIL to reject the null hypothesis. So there is no evidence to conclude that at least one mean of the groups differs significantly from the others.