Question

Find all zeros of f(x)=x^4-3x^3+6x^2+2x-60 given that 1+3i is a zero of f(x) ​

Answer 1

The roots of f(x) are: -2, 3, (1+3i) and (1-3i)

Explanation:

We are given an expression:

`f(x)=x^4-3x^3+6x^2+2x-60`

(1+3i) is a root of f(x)

We have to find the remaining roots of f(x).

Since, (1+3i) is a root of f(x),

`x-(1+3i)`

is a factor of given expression.

Now, we check if (1 - 3i) is a root of given function.

`f(x)=x^4-3x^3+6x^2+2x-60\\f(1-3i)=(1-3i)^4-3(1-3i)^3+6(1-3i)^2+2(1-3i)-60\\= (28+96i)-3(-26+18i)+6(-8-6i)+2(1-3i)-60 = 0`

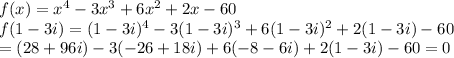
Thus, (1-3i) is also a root of given function.

Since, (1-3i) is a root of f(x),

`x-(1-3i)`

is a factor of given expression.

Thus, we can write:

`(x-(1+3i))(x-(1-3i))\text{ is a factor of f(x)}\\x^2-x(1-3i)+x(1+3i)+(1-3i)(1+3i)\text{ is a factor of f(x)}\\x^2-2x+10\text{ is a factor of f(x)}`

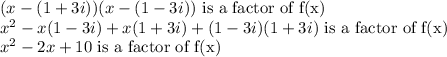
Dividing f(x) by above expression:

`\displaystyle(x^4-3x^3+6x^2+2x-60)/(x^2-2x+10) = x^2-x-6`

To find the root, we equate it to zero:

`x^2-x-6 = 0\\x^2 - 3x+2x-6=0\\x(x-3)+2(x-3)=0\\(x+2)(x-3) = 0\\x = -2, x = 3`

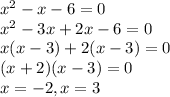
Thus, the roots of f(x) are: -2, 3, (1+3i) and (1-3i)