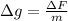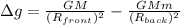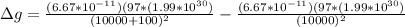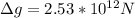Question

A spacecraft in the shape of a long cylinder has a length of 100 m,and its mass with occupants is 1490kg. It has strayed too close to a black hole having a mass97 times that of the Sun. The nose ofthe spacecraft points toward the black hole, and the distancebetween the nose and the center of the black hole is 10.0 km.

(a) Determine the total force on thespacecraft.
(b) What is the difference in the gravitational fields acting onthe occupants in the nose of the ship and on those in the rear ofthe ship, farthest from the black hole? This difference inacceleration grows rapidly as the ship approaches the black hole.It puts the body of the ship under extreme tension and eventuallytears it apart.

Answer 1

To develop this problem, it is necessary to apply the concepts related to the Gravitational Force and its respective change related to the black hole.

Gravitational Force are given as

`F = (GMm)/((R+l)^2)`

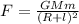
Where

l = Length

R = Separation between both

M = Mass of Object

m = mass of block hole

G = Gravitational Universal constant

Our values are given as

l = 100m

M = 1490

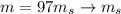`m = 97 m_s \rightarrow m_s` is mass of sun

R = 10km

PART A ) Replacing in our equation we have that

`F = (GMm)/((R+l)^2)`

`F = ((6.67*10^(-11))(1490)(97*(1.99*10^(30))))/((10000+100)^2)`

`F = 1.8805*10^(17)N`

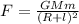
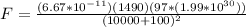
PART B) The difference at this force would be given as

`\Delta F = (GMm)/((R_(front))^2)-(GMm)/((R_(back))^2)`

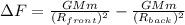
As Force is equal to mass and gravity then

`\Delta g = (\Delta F)/(m)`

`\Delta g = (GM)/((R_(front))^2)-(GMm)/((R_(back))^2)`

`\Delta g = ((6.67*10^(-11))(97*(1.99*10^(30)))/((10000+100)^2)-((6.67*10^(-11))(97*(1.99*10^(30)))/((10000)^2)`

`\Delta g = 2.53*10^(12)N`