Question

Suppose that x has a binomial distribution with n = 50 and p = .6, so that μ = np = 30 and σ = np(1 − p) = 3.4641. Calculate the following probabilities using the normal approximation with the continuity correction. (Hint: 22 < x < 37 is the same as 23 ≤ x ≤ 36. Round your answers to four decimal places.) g

Answer 1

Question:

Suppose that x has a binomial distribution with n = 50 and p = 0.6, so that μ = np = 30 and σ = np(1 − p) = 3.4641. Approximate the following probabilities using the normal approximation with the continuity correction. (Hint: 26 < x < 32 is the same as 27 ≤ x ≤ 31. Round your answers to four decimal places.)

(a) P(x = 30)

(b) P(x = 26)

(c) P(x ≤ 26)

(d) P(26 ≤ x ≤ 32)

(e) P(26 < x < 32)

Answer:

(a) P(x = 30)=0.1113

(b) P(x = 26)=0.8064

(c) P(x ≤ 26)=0.9032

(d) P(26 ≤ x ≤ 32)=0.6674

(e) P(26 < x < 32)=0.5101

Explanation:

Here , X has a binomial distribution with n= 50 and p=6

The mean is μ=np=50(0.6)=30

The standard deviation is
`\sigma=√(np(1-p))=\sqrt{50(0.6)(0.4)`

=>3.4641

(A) P(x = 30)

=>
`P(X_(Binomial)=30)= P(30-0.5\leq{normal}\leq30+0.5)`

=>
`P(29.5\leqY_(normal)\leq30.5)`

=>
`P((29.5-30)/(3.4641)\leq(Y_(normal)-\mu)/(\sigma)\leq(30.5-30)/(3.4641))`

=>
`P(-0.14\leqZ\leq0.14)`

=>
`P(z\leq0.14)- P(z\leq0.14)`

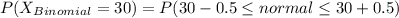
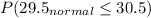
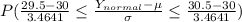
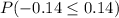
=>[=NORMSDIST(0.14)]-[=NORMSDIST(0.14)]

=>0.5557-0.4443

=>0.1113

(B)P(x = 26)

=>
`P(X_(Binomial)=26)= P(26-0.5\leqY_(normal)\leq26+0.5)`

=>
`P(25.5\leqY_(normal)\leq26.5)`

=>
`P((25.5-30)/(3.4641)\leq(Y_(normal)-\mu)/(\sigma)\leq(26.5-30)/(3.4641))`

=>
`P(-1.30\leq z \leq1.30)`

=>
`P(Z\leq1.30)- P(Z\leq1.30)`

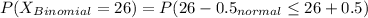
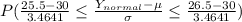
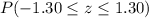
=>[=NORMSDIST(1.30)]-[=NORMSDIST(-1.30)]

=>0.9032-0.0968

=>0.8064

(c) P(x ≤ 26)

=>
`P(X_(Binomial)\leq26)= P(Y_(normal)\leq26+0.5)`

=>
`P(Y_(normal)\leq26.5)`

=>
`P((Y_(normal)- \mu)/(\sigma)\leq(26.5-30)/(3.4641))`

=>
`P(Z\leq1.30)`

=>
`P(Z\leq1.30)`

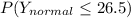
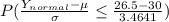
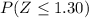
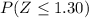
=>[=NORMSDIST(1.30)]

=>0.9032

D) P(26 ≤ x ≤ 32)

=>
`P(26\leqX_(Binomial)\leq32)= P(26-0.5\leqY_(normal)\leq32+0.5)`

=>
`P(25.5\leqY_(normal)\leq32.5)`

=>
`P((25.5-30)/(3.4641)\leq(Y_(normal)-\mu)/(\sigma)\leq(32.5-30)/(3.4641))`

=>
`P(-1.30\leqZ\leq0.72)`

=>
`P(Z\leq0.72)- P(Z\leq-1.30)`

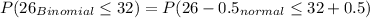
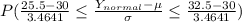
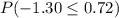
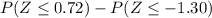
=[=NORMSDIST(0.72)]-[=NORMSDIST(-1.30)]

=>0.7642 -0.0968

=>0.6674

(E) P(26 < x < 32)

=>
`P(26<X_(Binomial)<32)= P(26-0.5<Y_(normal)<32-0.5)`

=>
`P(26.5<Y_(normal)<=31.5)`

=>
`P((26.5-30)/(3.4641)<(Y_(normal)-\mu)/(\sigma)<(31.5-30)/(3.4641))`

=>
`P(-1.01\leqz\leq0.43)`

=>
`P(Z\leq0.43)- P(Z\leq-1.01)`

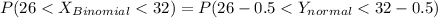
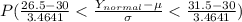
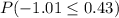
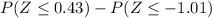
=>[=NORMSDIST(0.43)]-[=NORMSDIST(-1.01)]

=>0.6664-0.1563

=>0.5101