Question

Five hundred raffle tickets are sold for $3 each. One prize of $500 is awarded. Raul purchases one ticket. Determine his expected value

Answer 1

His expected value is -2

Explanation:

Five hundred raffle tickets are sold for $3 each

One prize of $500 is awarded.

Expected value =
`xP(x)`

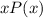
Probability of winning =
`(1)/(500)`

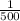
If won the price he gets = 500

But he also paid $3 to buy ticket

So, the actual price he got = 500-3= 497

Probability of not winning =
`(499)/(500)`

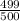
So, Expected value=
`(1)/(500)(497)+(499)/(500)(-3)`

=
`-2`

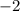
Hence his expected value is -2