Answer:
We have the equation
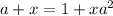
we leave the terms with x on the left side of the equation and the independent terms on the right side.
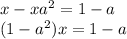
resolving for x we have that
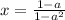
Since we need that the equation doesn't have solution, then it is necessary that the denominator of x be 0 and this occur when

Then, for
 the equation hasn't solution
the equation hasn't solution