Answer:
K = 113.55 J
Step-by-step explanation:
Newton's second law:
F = ma has the equivalent for rotation:
τ = I * α Formula (1)
where:
τ : It is the moment applied to the body. (Nxm)
I : it is the moment of inertia of the body with respect to the axis of rotation (kg*m²)
α : It is angular acceleration. (rad/s²)
Calculation of the torque (τ) applied to the merry-go-round
τ = F * R Formula (2)
Where :
F is the tangential force in Newtons (N)
R is the radio , perpendicular to F
Data
F=51.0 N
R = 1.51 m
We replace data in the formula (2)
τ = F * R
τ = 51.0 N * 1.51 m = 77.01 N*m
Moment applied to the merry-go-round:
The moment of inertia of a solid disk that rotates around an axis that passes through its center is::
I = (1/2)m*R² Formula (3)
Where:
I: moment of inertia of the solid disk ( kg*m²)
m : mass (kg)
R : disk radio
Data
W=810 N :weight of the merry-go-round
W= m*g
g= 9.8 m/s² = acceleration due to gravity
m = W/g =810/ 9.8
m = 82.65 kg : mass of the merry-go-round
R = 1.51 m : radio of the merry-go-round
We replace data in the formula (3)
I = (1/2)(82.65)*(1.51)²
I = 94.23 kg*m²
Angular acceleration of the merry-go-round
We replace data in the formula (1):
τ = I * α
77.01= 94.23 * α
α= 77.01 / 94.23
α = 0.8173 rad/s²
Kinetic energy of the merry-go-round disk
K = (1/2) I *ω² Formula (4)
where:
K : rotation kinetic energy (J)
I : Moment of inertia of the body with respect to the axis of rotation (kg*m²)
ω: Angular speed (rad/s)
Kinematics of the merry-go-round
We apply the equations of circular motion uniformly accelerated:
ω²= ω₀+α*t Formula (5)
Where:
α : Angular acceleration (rad/s²)
ω₀ : Initial angular speed ( rad/s)
ω : Final angular speed ( rad/s)
t : time interval (s)
Data
α = 0.8173 rad/s²
ω₀ = 0
t = 2.95 s
We replace data in Formula (5)
ω²= ω₀+α*t
ω²= 0+ (0.8173) *(2.95)
ω²= 2.41
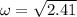
ω = 1.55 rad/s
We replace I = 94.23 kg*m² and ω = 1.55 rad/s in the formula (4):
K = (1/2) (94.23)*(1.55)²
K = 113.55 J