To solve this exercise it is necessary to apply the concepts given in the Faraday expressions and the induced voltage.
By definition the emf is given under the equation
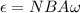
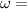 Angular Velocity
Angular Velocity
N = Number of Loops
B = Magnetic Field
A = Cross-Sectional Area.
At the same time we know that the rate of energy delivered is defined as,
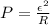
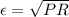
Re-arrange the firs equation to find the number of loops and replacing the definition previously found we have,
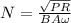
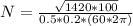
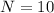
Therefore the number of turns in the coild if energy is delivered to it at a maximum rate of 1420W are 10 loops.