1 Answer

Habibalsaki · Answer 1 · 2020-06-24T09:22:14+0000

Answer:

m∠DEC = 78°

Explanation:

Given information: AC = AD, AB⊥BD, m∠DAC = 44° and CE bisects ∠ACD.

If two sides of a triangles are congruent then the opposite angles of congruent sides are congruent.

AC = AD (Given)

$\angle ADC\cong \angle ACD$

$m\angle ADC=m\angle ACD$

According to the angle sum property, the sum of interior angles of a triangle is 180°.

$m\angle ADC+m\angle ACD+m\angle DAC=180$

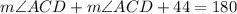
$m\angle ACD+m\angle ACD+44=180$

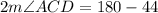
$2m\angle ACD=180-44$

$2m\angle ACD=136$

Divide both sides by 2.

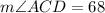
$m\angle ACD=68$

CE bisects ∠ACD.

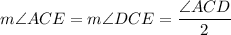
$m\angle ACE=m\angle DCE=(\angle ACD)/(2)$

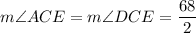
$m\angle ACE=m\angle DCE=(68)/(2)$

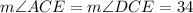
$m\angle ACE=m\angle DCE=34$

Use angle sum property in triangle CDE,

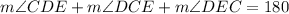
$m\angle CDE+m\angle DCE+m\angle DEC=180$

$68+34+m\angle DEC=180$

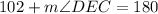
$102+m\angle DEC=180$

Subtract 102 from both sides.

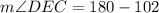
$m\angle DEC=180-102$

$m\angle DEC=78$

Therefore, the measure of angle DEC is 78°.

Please log in or register to add a comment.