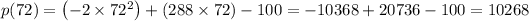Question

The revenue (in dollars) for selling q items is given by R ( q ) = 348 q − 2 q 2 and the costs (in dollars) of producing q items is given by C ( q ) = 100 + 60 q . Find the quantity that gives the maximum profit.

Answer 1

The quantity of 72 that gives the maximum profit of 10268

Step-by-step explanation:

The profit function p(q) is given by the difference between the revenue and the cost function,

P(q) = R(q) - C(q)

The revenue (in dollars) for selling q items is given by
`R(q)=348 q-2 q^(2)`

The costs (in dollars) of producing q items is given by C(q)= 100 + 60q

`P(q)=348 q-2 q^(2)-(100+60 q)`

`=348 q-2 q^(2)-100-60 q`

`=-2 q^(2)+288 q-100`

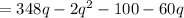
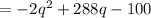
The above profit function is a downward opening parabola. Its maximum value occurs,

`\text { At } x=-(b)/(2 a)=-(288)/(2(-2))=72`

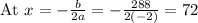
Maximum value,
`p(72)=\left(-2 * 72^(2)\right)+(288 * 72)-100=-10368+20736-100=10268`