Question

The town of Hayward (CA) has about 50,000 registered voters. A political research firm takes a simple random sample of 500 of these voters. In the sample, the breakdown by party affiliation is 115 Republicans, 331 Democrats, and 54 Independents. Calculate a 98% confidence interval for the true percentage of Independents among Haywards 50,000 registered voters.

Answer 1

Answer: (0.076, 0.140)

Explanation:

Confidence interval for population proportion (p) is given by :-

`\hat{p}\pm z_(\alpha/2)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

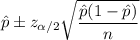
, where
`\hat{p}` = sample proportion.

n= sample size.

`\alpha` = significance level .

`z_(\alpha/2)` = critical z-value (Two tailed)

As per given , we have

sample size : n= 500

The number of Independents.: x= 54

Sample proportion of Independents
`\hat{p}=(x)/(n)=(54)/(500)=0.108`

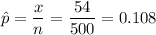
Significance level 98% confidence level :
`\alpha=1-0.98=0.02`

By using z-table , Critical value :
`z_(\alpha/2)=z_(0.01)=2.33`

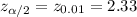
The 98% confidence interval for the true percentage of Independents among Haywards 50,000 registered voters will be :-

`0.108\pm (2.33)\sqrt{(0.108(1-0.108))/(500)}\\\\=0.108\pm2.33*0.013880634\\\\=0.108\pm0.03234187722\\\\\approx0.108\pm0.032=(0.108-0.032,\ 0.108+0.032)=(0.076,\ 0.140)`

Hence, the 98% confidence interval for the true percentage of Independents among Haywards 50,000 registered voters.= (0.076, 0.140)