Answer:
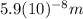
Step-by-step explanation:
The equation to calculate the center of mass
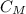 of a particle system is:
of a particle system is:
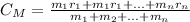
In this case we can arrange for one dimension, assuming the geometric center of the Earth and the ladder are on a line, and assuming original center of mass located at the Earth's geometric center:
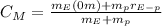
Where:
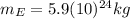 is the mass of the Earth
is the mass of the Earth
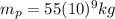 is the mass of 1 billion people
is the mass of 1 billion people
 is the radius of the Earth
is the radius of the Earth
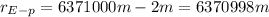 is the distance between the center of the Earth and the position of the people (2 m above the Earth's surface)
is the distance between the center of the Earth and the position of the people (2 m above the Earth's surface)
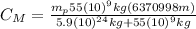
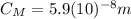 This is the displacement of Earth's center of mass from the original center.
This is the displacement of Earth's center of mass from the original center.