Answer:
nth term =

Explanation:
Let us assume that the given sequence is a G.P.
Now, if the first term of the G.P. is a and the common ratio is r, then
Third term =
 .......... (1) and
.......... (1) and
20th term =
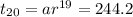 ........... (2)
........... (2)
Now, dividing equation (2) with equation (1) we get
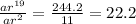
⇒
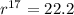
⇒ r = 1.2.
Hence, from equation (1) we get
a(1.2)² = 11
⇒ a = 7.639 (Approx.)
Therefore, the general term of the sequence i.e. nth term =
 (Answer)
(Answer)