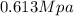Question

A spherical balloon is made from a material whose mass is 2.70 kg. The thickness of the material is negligible compared to the 1.55 m radius of the balloon. The balloon is filled with helium (He) at a temperature of 290 K and just floats in air, neither rising nor falling. The density of the surrounding air is 1.19 kg/m³ and the molar mass of helium is 4.0026×10-3 kg/mol. Find the absolute pressure of the helium gas.

Answer 1

To develop this problem it is necessary to apply the concepts related to the calculation of the Force through density and volume as well as the ideal gas law.

By definition, force can be expelled as

F = ma

Where,

m = mass

a = Acceleration

At the same time the mass can be defined as function of density and Volume

`m = \rho V`

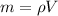
Therefore if we do a sum in the spherical balloon we have,

`\sum F = 0`

`F_w +F_h-F_b=0`

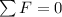
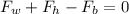
Where,

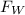`F_W`= Force by weight of balloon

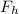`F_h`= Force by weight of helium gas

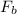`F_b`= Buoyant force

`mg + V \rho g - V\rho_a g = 0`

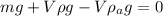
Re-arrange to find
`\rho,`

`\rho = \rho_a - (m)/(V)`

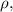
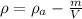
Our values are given as,

`r= 1.55m`

`V = (4)/(3) \pi r^3`

`V = (4)/(3) \pi (1.55)^3`

`V = 15.59m^3`

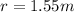
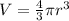
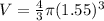
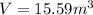
Replacing the values we have,

`\rho = 1.19kg/m^3 - (2.7)/(15.59)`

`\rho = 1.0168kg/m^3`

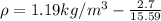
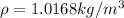
Applying the ideal gas law we have finally that

`P = (\rho)/(M_0) RT`

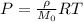
Where,

P = Pressure

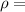`\rho =` Density

M_0 Molar mass (0.004Kg/mol for helium)

R= Gas constant

T = Temperature

Substituting

`P = (1.0168)/(0.004) *8.314*290`

`P = 612891.452Pa`

`P = 0.613Mpa`

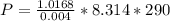
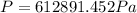
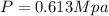
Therefore the absolute pressure of the helium gas is
`0.613Mpa`