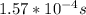Question

An unstable particle is created in the upper atmosphere from a cosmic ray and travels straight down toward the surface of the earth with a speed of 0.99542 c relative to the earth. A scientist at rest on the earth's surface measures that the particle is created at an altitude of 47.0 km .

Part A As measured by the scientist, how much time does it take the particle to travel the 47.0 km to the surface of the earth?

Answer 1

To solve this problem, it is necessary to apply the concepts related to speed of light and the kinematic equations of speed description.

The speed by definition can be expressed as the path of a particle during a certain time, in our case,

`v = (d)/(t)`

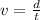
Where,

d= distance

v = speed

c = Speed of light
`(3*10^8m/s)`

Replacing to find the time we have,

`t=(d)/(v)`

`t = (47000)/(0.99542*(c))`

`t = (47000)/(0.99542*(3*10^8))`

`t = 1.57*10^(-4)s`

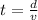
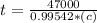
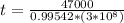
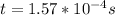
Therefore the time is
`1.57*10^(-4)s`