Question

On a hot summer day, the density of air at atmospheric pressure at 31.5°C is 1.2074 kg/m3.

(a) What is the number of moles contained in 1.00 m3 of an ideal gas at this temperature and pressure? mol
(b) Avogadro's number of air molecules has a mass of 2.88 ✕ 10−2 kg. What is the mass of 1.00 m3 of air? (Assume air is an ideal gas.) kg
(c) Does the value calculated in part (b) agree with the stated density of air at this temperature? (Consider that it does if the values are within 10% of each other.) Yes

Answer 1

To solve this problem, it is necessary to apply the ideal Gas equations, as well as the calculation equations of the weight difference, which under the comparison of two values.

By definition we know that the ideal gas equation is given by the equation,

PV = nRT

Where,

P = Pressure

V = Volume

R = Gas ideal constant

T = Temperature

n = number of moles

Our values are given by

`P = 1.1013*10^5Pa`

`T = 31.5\°C = 304.5K`

`\rho = 1.2074kg/m^3`

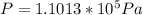
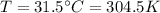
PART A) Using this previous equation we can find the number of moles per Volume, that is

`PV = nRT`

`(n)/(V) = (P)/(RT)`

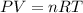
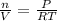
Replacing with our values

`(n)/(V) = (1.013*10^5)/((8.314)(304.5))`

`(n)/(V) = 40.014mol/m^3`

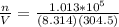
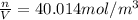
PART B ) We can calculate the number of moles of 1m^3 through Avogadro number, then

`M = nA`

`M = 40.014*(2.88*10^(-2))`

`M = 1.1524Kg`

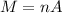
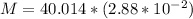
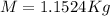
Therefore in
`1m^3` there are 1.1524Kg of Gas.

PART C ) Density can be defined as the proportion of mass in a specific quantity of Volume, then

`\rho_2 = (M)/(V)`

`\rho_2 = (1.1524)/(1)`

`\rho_2 = 1.1524kg/m^3`

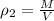
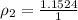
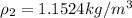
The difference of percentage then is

`\Delta \rho = (\rho_1-\rho_2)/(\rho_2)*100\%`

`\Delta \rho = (1.2074-1.1524)/(1.1524)*100\%`

`\Delta \rho = 0.0477*100\%`

`\Delta \rho = 4.77\%`

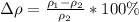
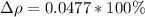
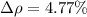
YES, because as the percentage is less than 10%, the calculated value agrees with the stated value.