Question

Can someone help me with this problem asap

Answer 1

f(x) =
`$ x^4 - 2x^3 + 49x^2 - 18x + 360 $` is the required polynomial.

Explanation:

Given the zeroes (roots) of the polynomial are
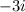`$ -3i $` and
`$ 2 + 6i $`.

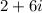We know that complex roots occur in conjugate pairs.

So, this means that
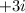`$ +3i $` and
`$ 2 - 6i $` would also be the roots of the polynomial.

If
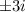`$ \pm 3i $` are to be the roots of the polynomial then the polynomial should have been:
`$ x^2 + 9 = 0$`.

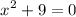Now, to determine the polynomial for which
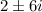`$ 2 \pm 6i $` would be the roots.

Roots of the polynomial are nothing but the values of x (any variable) that would make the polynomial zero.

⇒
`$ x = 2 + 6i \hspace{35mm} x = 2 - 6i $`

⇒
`$ x - 2 - 6i = 0 \hspace{25mm} x - 2 + 6i = 0 $`

The required polynomial would be the product of all the above polynomials.

`$ i.e., (x^2 + 9)(x - 2 + 6i)(x - 2 - 6i) = 0 $`

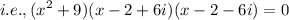
Multiply this to get the required equation.

⇒
`$ (x^2 + 9)(x^2 - 2x + 40) $`

`$ \implies x^4 - 2x^3 + 40x^2 + 9x^2 - 18x + 360 = 0 $`

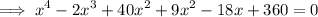
∴ The required polynomial is x⁴ - 2x³ + 49x² - 18x + 360 = 0.