Question

A solenoid with 33 turns per centimeter carries a current I. An electron moves within the solenoid in a circle that has a radius of 2.1 cm and is perpendicular to the axis of the solenoid. If the speed of the electron is 3.6 ✕ 105 m/s, what is I (in A)?

Answer 1

To develop this problem it is necessary to match the concepts related to electromagnetic force and the centripetal Force.

By definition we have that the centripetal Force is equivalent to

`F_c = (mv^2)/(R)`

Where,

m = Mass (of a electron)

v = Velocity

R = Radius

At the same time we have that magnetic force is equal to

`F_e = qvB`

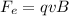
Where,

q = Charge

V = Velocity

B = Magnetic Field

Equating both we have,

`F_c = F_e`

`(mv^2)/(R) = qvB`

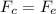
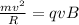
Re-arrange to find B,

`B = (mv)/(qR)`

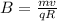
Replacing with our values we have,

`B = ((9.1*10^(-31))(3.6*10^5))/((1.6*10^(-19))(2.1*10^(-2)))`

`B = 0.0000975T`

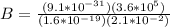
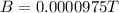
Now for Faraday's law the Magnetic field in a solenoid is defined as,

`B = \mu_0 NI`

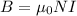
Re-arrange to find I

`I = (\B)/(\mu N)`

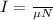
Where,

B = Magnetic Field

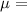`\mu =` Permeability constant

N = Number of loops per meter

Replacing with our values

`I = ((0.0000975))/((4\pi*10^(-7))(3300))`

`I = 0.235115A`

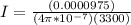
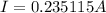
Therefore the Current is 0.235115A