Question

A new roller coaster contains a loop-the-loop in which the car and rider are completely upside down. If the radius of the loop is 11.8 m, with what minimum speed must the car traverse the loop so that the rider does not fall out while upside down at the top? Assume the rider is not strapped to the car.

Answer 1

To solve this problem it is necessary to apply the concepts based on Newton's second law and the Centripetal Force.

That is to say,

`F_c = F_w`

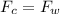
Where,

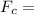`F_c =`Centripetal Force

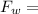`F_w =`Weight Force

Expanding the terms we have to,

`mg = (mv^2)/(r)`

`gr = v^2`

`v = √(gr)`

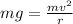
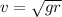
Where,

r = Radius

g = Gravity

v = Velocity

Replacing with our values we have

`v = √((9.8)(11.8))`

`v = 10.75m/s`

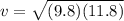
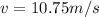
Therefore the minimum speed must the car traverse the loop so that the rider does not fall out while upside down at the top is 10.75m/s