Question

A two slit interference/diffraction pattern is set up (thus for this problem we will take into account the effects of both diffraction and interference). You are given that the screen is 1.8 m away from the slits with width .01 mm and spacing .05 mm and light of wavelength 640 nm is used. What is the smallest order interference maximum that is "missing" from the interference/diffraction pattern on the screen?

Answer 1

To solve this problem it is necessary to apply the concepts related to interference (destructive and constructive), as well as to the principle of overlap.

By definition we know that constructive interference is defined as

`dsin\theta = m\lambda`

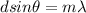
Where,

d = Distance between slits

m = Order interference (Representing the number of repetition of spectrum)

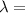`\lambda =` wavelength

Re-arrange the equation to find the angle with the minimum order (m=1) we have,

`\theta = sin^(-1) ((m *\lambda)/(d))`

`\theta = sin^(-1)((1 * 640 * 10^(-9))/(0.01*10^(-3)))`

`\theta = 3.6690\°`

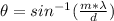
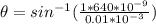
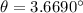
For the order of the missing interference we can calculate with the spacing of 0.05mm:

`m = (d * sin\theta)/(\lambda)`

`m = (0.05 * 10^(-3)* sin 3.669)/(640 * 10^(-9))`

`m = 4.99 = 5`

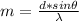
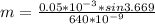
Therefore the smallest order interference maximum that is 'missing' from the interference/diffraction pattern on the screen is 5.